Matematika hitza entzuten dugunean, gure buruan eraikuntza zehatz bat sortu ohi da. Garaiko matematika zerbait zehatza dela esan eta sinestarazi digute: “argi dago, bat gehi bat bi da”, “argi dago, minus baten erroa zenbaki konplexuaren zati irudikaria da”, “argi dago, …”. Baina hori batzuen ikuspuntua besterik ez da, eta ez da ingurua ulertzeko modu bakarra.
Bizi dugun kulturak matematika mota bat erakusten digu. Matematikak inguruaren eraikuntzan du eragina eta inguruak matematikarenean, hau da, ingurua ikusteko duzun moduaren arabera sortuko edo erabiliko duzu matematika. Artean gertatzen den bezala, matematikak fikziozko munduak sortzen ditu, eta fikzio horiek errealitateak ere eratzen ditu; era berean, modu itxian erakusten diguten matematikak pentsatzeko moduak sortzen ditu. Baieztapen horren muinak egunerokotasunean pentsatzen duguna baino indar handiagoa du.
Adibidez, gure kulturan hutsa ez da ezer, baina Txinan, aldiz, hutsa betearen osagarria da, betearen konplementarioa! Ikuspuntu horretatik hutsak badu presentzia, beraz. Beraientzat zheng (gure zenbaki positiboa) eta fu (gure zenbaki negatiboak) kontrakoak dira; biak dira naturalak, oposizioa baita naturala haien kulturan, yin-a eta yang-a. Baina guretzat, ez; guretzat naturalena zenbaki positiboak dira. 1 zenbakiak “+1” adierazten du, baina “+” horrek ez digu informaziorik ematen, hemen naturalena zenbaki positiboa izatea baita. Zenbaki negatiboa adierazi nahi badugu, orduan minus zeinua jarri behar diogu. Hau ez da izan/ez-izan edo banaketa bat, biak daude presente txinatarrentzat eta bien arteko zubiak daude; era horretan, bidean aukerak zabaltzen dira, bi aukera aurkariak eduki beharrean.
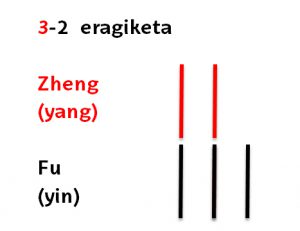Kenketak egiteko garaian ezagutzen ditugun ebasketak egin beharrean bikoteak egiten dituzte, yin eta yang zenbakien arteko bikoteak. Haiek mahaiaren gainean makilatxo negatiboak jartzen dituzte, hau da, zenbaki horiei entitatea ematen diote. Beraien 2-3 kenketa egiteko lurrean 2 makilatxo yang (gorriak) jarriko genituzke eta behean 3 makilatxo yin (beltzak).
Yin eta yang makila bikoteak beraien artean deuseztatzen dira, beraz, 2 makilatxo yang eta bi makilatxo yin desagertuko dira eta bikoterik gabe geratzen dena yin makil beltz bat da, hau da, bat zenbakiaren yin izaera: gure -1.
Emmanuel Lizcanok Las matemáticas de la tribu europea: Un estudio de caso dokumentuan, besteak beste, Yoruba aritmetika eta “aritmetika demokratikoaren” arteko desberdintasuna adierazten du. Yoruba hiztunentzat, kontatzeko unitatea ez da banan bana pertsonak kontatzeko erabiltzen dugun “bat” zatiezin hori. Unitate aritmetikoa unitate sozialarekin du zerikusia, unitate kolektiboa, hau da, singular kolektiboa. Yoruba zenbakiak ez dira adjektiboak edo adjektibo substantiboak, aditzak dira. Hala, haien zenbaki sistema ez da batarekin hasten, elementu multzoekin hasten da (hogei, hamar eta bosteko unitateetan) eta kenketen bitartez multzo horien zatiak sortzen dira. “Aritmetika demokratiko”-ekin zenbatutako bat unitario homogeneo “berdinak” unitate kolektiboen aurrean. Emmanuelek zera gehitzen du “txikitatik ikasi ditugun ‘zenbaki naturalak’ ez dira hain naturalak… Bere naturaltasuna eraikuntza sozial zehatz batekin du zerikusia”.
Zinez interesgarriak dira goian dituzuen erreferentziatan agertzen diren azalpen sakon guztiak bai eta Emmanuel Lizcanoren hitzaldi hau.
Asko esaten dugu matematikak irakasteko moduarekin, asko, sortzen eta sortarazten gaituen kulturi buruz (eta alderantziz) eta, noski, guzti horrek elkarren arteko harremanekin, ezartzen diren politikekin eta botereekin du zerikusia ere. Adi egon matematikei eta horien transmisioa eragiten dutenei. Matematika bakarra onartzen badugu, pertsona batzuen eskutan dagoen zientzia klasista bakarra onartzen badugu, botereari indarrak emango dizkiogu eta bazterkeria indartu, ingurua ulertzeko modu bat bultzatuko baitugu, unitate kolektibo, komunitario edo sozial anitzen deuseztatzeko bideari hegoak emanaz.
Etzi gaur da.
Irudia: Partitura librea – Arkaitz Barriola “Matematikak, fikziozko mundu anitzak” testuan oinarrituta.
